Compliance Analysis
Please enjoy the 2-minute summary gallery below, or scroll further to explore my work in greater detail
Suspension performance is critically dependent on the kinematic control of linkages in 3-D space. However, since a truly rigid body does not exist, suspension links inevitably deform under the various loads cases seen on the track, which can affect the performance and stability of the vehicle. Further adding to the challenge is the opposing criteria of minimizing mass of suspension components, which will decrease their stiffness.
Compliance is a notoriously ignored phenomenon in the Formula SAE community, to the frustration of many design judges who have made it a core topic of technical discussion. The Clemson FSAE team has been historically guilty of this, but over the last couple of years I have led a foray into the exploration of its effects in a push to develop more informed design targets. In this page, you will see my discussion on my development work to date, as well as the critical validation steps that need to be made and future development routes that I would like to explore.
Clemson FSAE's 2019 car, Tiger21, was the first to be developed with suspension compliance targets in mind.
Overall Approach
For this initial foray into compliance exploration, I wanted to focus my efforts on two significant areas affecting performance and stability: camber and toe compliance in cornering scenarios. This is not to say that there aren't other important areas of compliance management; for example, vertical force load paths in the suspension and mounting are often some of the most egregious sources of compliance! Camber and toe errors simply have a more directly calculable effect on the performance and stability of the vehicle, and provide a solid foundation for a first exploration.
That's not to say that other sources of compliance were ignored, either! The first and most significant step in controlling compliance comes from managing load paths from the suspension into the chassis. No amount of link sizing optimization will mitigate the deflection of a rod end in bending, mounted in single shear to a non-nodal cantilevered frame post. I won't go into too much detail here, but there are other pages on this site where you can read more about the conceptual, packaging and mounting decisions made across the suspension to minimize compliance
One quick example of load path management - when exploring different spring concepts for the Tiger22 decoupled suspension, the final decision was to use an anti roll bar mounted to the pitch rocker. One of the driving factors behind this decision was that by consolidating most of the loads onto one of the rockers, we'd minimize the torsion loads, and therefore deflection, across the rocker shaft.
Load paths being set aside, the approach to selecting compliance targets began with exploring the effects of compliance on steady state performance, cornering response, and vehicle control. Alongside that, I used suspension load cases and basic sizing calculations to build a rough correlation between a compliance target, and the subsequent weight of a suspension sized properly to achieve that. Since compliance was a new area, we did not have previous data or targets to inform a threshold for how much compliance is too much compliance. Instead, my approach was to consider the compliance and weight trade-off hand in hand, and balance their respective points of diminishing returns to select final targets.
Toe Compliance Analysis
Since steering is the direct cornering "control" input at the driver's disposal, toe (or steering) compliance has a significant effect on vehicle behavior deviations. For both front and rear, toe compliance has a direct effect on the slip angles achieved in a corner, which can drastically alter vehicle balance or outright performance if not managed properly.
My initial analysis was done with a linear bicycle model using the Bundorf Cornering Compliance concept pioneered by R. Thomas Bundorf (Bundorf, R. and Leffert, R., "The Cornering Compliance Concept for Description of Vehicle Directional Control Properties," SAE Technical Paper 760713, 1976). This is because the 2 degree of freedom bicycle model is a powerful tool to explore basic control and stability parameters, and using cornering compliance to describe front/rear axle performance makes incorporating added compliance very straightforward.
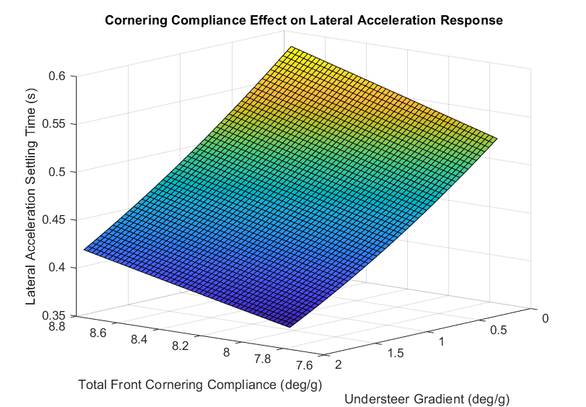
The following figure was generated using a step-steer simulation to explore the effects of compliance on cornering response time. It is apparent that increasing compliance overall hurts response. However, increasing understeer compliance has a much larger effect in improving response! This is because the rear axle provides the stabilizing yaw moment in a corner, and the stronger it is relative to the front the faster it will be able to "catch" the car.
Under-steer, however, is a double edged sword. Firstly, there are other ways to achieve understeer, such as tuning the lateral load transfer distribution or static camber alignment. In addition, excessive under-steer hurt peak lateral performance capacity due to the front axle saturating much sooner than the rear. Lastly, vehicle balance is a key drive-ability parameter, and we have testing data informing our understeer gradient targets based on driver preference. Straying away from that target would need some serious justification.
To explore the control of the vehicle, step steer inputs are inadequate in capturing the hysteresis effects of compliance. FSAE tracks typically feature several slalom sections, and this would be an area where hysteresis can have a large effect. The use of a linear model enabled a frequency response analysis to capture the on-center behavior of the car in such a situation.
This bode plot captures the frequency response of the vehicle for an average FSAE track slalom speed, across a range of typical slalom steering input frequencies
One concern of mine was that the cornering compliance model was not properly capturing the hysteresis/oscillation effect of toe compliance as a spring element. So I took the effort to expand a traditional 2 DoF bicycle (using cornering stiffness) into 6 degrees of freedom, incorporating toe by modelling the unsprung mass motion with an inertia and rotational spring element. The results ended up correlating very closely to the original model, which gave me the confidence to continue. Moving forward, I continued to utilize the cornering compliance model since it provided a simple, normalized representation of compliance without having to worry about specific inertia and stiffness values.
Upon initial inspection, there are no drastic changes in the shape of the vehicle response behavior in any modes. However, vehicle sideslip angle gain at low frequencies does increase in magnitude significantly with more compliance. Vehicle sideslip response is a key driver feedback mechanism, so this effect may be noticeable by an experienced driver. Beyond that, it looks like changes in vehicle behavior correlate roughly linearly with increased compliance. This pattern continues for higher ranges of compliance, shown by the figure below.
Sideslip set aside, increased compliance has a direct effect on diminishing the yaw velocity and lateral acceleration gain, implying a loss of total responsiveness. In addition, around an input frequency of 1 Hz, the lateral acceleration phase has significant divergence. These are both effects that we want to minimize, but there are no clear thresholds of diminishing returns present.
Further insight can be found by exploring the isolated contributions of front and rear compliance, respectively:
There is little surprise that each axle has opposite effects, as the front axle is the control/destabilizing axle and the rear axle is the stabilizing axle. What is more interesting is that the front end has a higher net effect on the acceleration and yaw response, while the rear end is more significant in the sideslip response. This is because steady state lateral velocity is directly tied to rear cornering stiffness, with little to no effect from the front. It is useful here that the front end is more significant in determining the yaw response, where compliance will have a slight stabilizing effect.
Frequency response plot, replicated using my expanded model
Toe Compliance Continued: Nonlinear Analysis
In typical vehicle modeling, treating the tire as a linear spring can help simplify analysis for small perturbations and lateral accelerations, and provide a useful framework for exploring limit behavior (with care). However, with compliance, there are far more sources of non-linearity. Tire lateral force has a nonlinear relationship with slip angle, but so does the vertical returning moment, which in fact reaches a negative stiffness after a certain threshold. On top of that, steering system compliance has many sources of nonlinearity, from U-joint angles to steering arm alignment and rack offset. Because of this, I felt the need to expand to a nonlinear representation in order to evaluate limit behavior using a quasi-steady state approach.
Demonstration of tire nonlinearity. Units are omitted to meet intellectual property requirements.
One of the first interesting insights is to explore the propagation of understeer with increasing compliance. It is a natural phenomenon that understeer increases near the limit, as the front tires reach their saturation point before the rears. However, this effect is exacerbated by the introduction of toe compliance. Another interesting trend is the 'waviness' of the UG curve. This is because the tire MZ saturation point and FY saturation point come at different slip angles. Since the vehicle is statically understeer biased, these saturation points will vary. This means that even though front and rear compliance have the same static value, their relative propagation will deviate. Overall though, the general shape of the curve is maintained.
Another useful way to visualize this data is from the more traditional understeer plot. With total compliance being equal front to rear, peak cornering capacity doesn't change, but the figure below demonstrates how much extra steering lock is required, and how that last bit of performance may be less accessible.
These nonlinear results demonstrate a phenomenon that would not have been apparent from the linear cornering compliance model. For most of the vehicle's lateral acceleration range, toe compliance actually has very little effect on steady state results. However, at the handling limit, toe compliance has a very significant effect, where the limit understeer gradient is magnified. This could be very noticeable, and potentially frustrating, to a driver, creating a further incentive to minimize compliance.
Steady state sideslip results don't add that much more information, but are quite interesting to look at. The shape of the curve changes based on whether the vehicle is travelling above or below its tangent speed.
As far as step input response goes, similar trends remain, although the response penalty is less drastic than the linear model.
Camber Compliance Analysis
Before we cover target selection, I want to move on to camber compliance modeling. Since camber relies on the roll and heave motions of the suspension, as well as lateral load transfer, a bicycle model is no longer useful. As a starting point, I built off of the 2 track kinematic model used to evaluate the effect of roll center heights. I then added extra degrees of freedom to capture camber deflection, once again using the inertia of the unsprung mass and treating suspension stiffness as a rotational spring element.
Whenever possible, I like to use only as much detail as necessary to capture the effects of a vehicle parameter, so that other factors do not cloud the results. This can include roll stiffness, damping and roll center effects. In this case, I had to model these effects in order the load transfer and cornering dynamics, using target values that had already been finalized. This should be taken as a caveat, and a future area of development may be to evaluate the sensitivity of camber compliance to roll and load transfer.
The plot below summarizes the step steer analysis carried out:
It is clear here that camber compliance has a very direct effect on hurting the responsiveness of the vehicle, while also having a slight effect on steady state performance. However, there is a clear case of diminishing returns this time, as compliance effects are minimal under 0.5 deg/g/
Overall, I did not spend as much time on camber compliance as I did toe. This is for two reasons. Firstly, toe has a direct effect on steered angles and slip angles of the tire, and therefore a more direct correlation to tire performance. Camber, on the other hand, though important, is more of a second-order effect. In addition, the stability sensitivity analysis I carried out when developing aero platform targets suggested camber to have very small effects on stability and response (I should specify, for the small deviations considered in this context). Secondly, steering is the direct control element at the driver's disposal, so any toe compliance will have a more direct effect on the control behavior of the vehicle.
Weight Effects and Target Selection
To predict weight requirements, I treated the suspension as a simplified assembly of two control arms, a steering link and a steering column (for a single corner). Load cases were generated using the same calculator used in control arm geometry development, with the links modeled as rigid truss elements. From there, simple stress strain and deflection calculations were carried out in Excel. This is a very, very simplified representation of a physical suspension. The purpose was not to perfectly predict the required weight to achieve a compliance target, but to visualize the general relationship between the two. The results are plotted below:
Both plots demonstrate a clear relationship of diminishing returns. Very low compliance values correspond to an exponential increase in component weight, with the curve quickly flattening out to the right. The control arm curve flat-lines because at that point, any smaller control arm would exceed the stress limits for our fatigue targets.
For the most part, the effects of compliance on performance and drive-ability were generally linear, while weight effects demonstrated more significant trade-offs. This informed our final decision, selecting compliance targets that were just above the threshold for significant weight increases. We ultimately decided that a camber and toe compliance range of 0.5/.35 deg/g, respectively, were acceptable values based on these sensitivity analyses. To keep a factor of safety and account for uncertainty, the final selected targets were 0.375 deg/g of camber compliance, and 0.25 deg/g of toe compliance.
This table summarizes these targets, how the targets were distributed by component, and then final expected component distribution. Some components overshot their target while others came in well below - these discrepancies will be used to refine future targets.
In addition, rear compliance turned out lower than front compliance, especially in toe deflection. This was deemed acceptable as it introduced a margin of stability, considering the uncertainty of these first compliance targets.
Refinements and Future Work
I am generally proud of the work done here. However, this is very much only a first step, and there is much work that still needs to be done to improve our understanding and control of compliance.
Firstly, physical measurements are a necessity. Ideally, we would have access to a K&C rig, but such resources are not always available to an FSAE team. Instead, there are much simpler isolated tests than can be run in the shop using simple fixtures and calibrated loads to measure deflection. This was planned to happen in spring of 2020, until the COVID-19 outbreak said otherwise.
Physical compliance data is important for two reasons. Firstly, it will be critical to correlating deflection predictions to actual values. Secondly, as I mentioned earlier, physical deflection is very nonlinear, especially in the steering system. Measuring the hysteresis and nonlinearity of steering column deflection can provide valuable data to refine the compliance models used above.
Secondly, physical part modeling needs to improve. For our 2020 compliance targets, parts were simulated individually in FEA, with total results coming from the summation of all parts. To our credit, this included bearing clearance and deflection. However, this is not an ideal way to capture compliance when all of these parts are interacting in a system. In the future, we will need to develop full FEA assemblies to capture the total system deflection, as opposed to taking a part-by-part approach.
Lastly, there are more opportunities to explore in compliance modelling. More work can be done in the evaluation of vertical spring load path compliance, and its effects on ride oscillations and roll/pitch stiffness. In addition, another area to explore would be using rear compliance to induce understeer to our advantage. This can help improve cornering response time and stability without having to hurt front end grip. This can be seen in the plot below:
In addition, rear induced compliance can achieve target understeer and stability metrics without the extreme UG saturation that results from front toe compliance. Compare these two side by side:
Of course, there are other ways to achieve this too, such as utilizing roll-steer. But nonetheless, this is a potentially exciting path to explore, and I am excited to continue my development in compliance analysis.



