Lap Time Simulation
Please enjoy the 2-minute summary gallery below, scroll further to explore my work in greater detail,
or explore my code in this GitHub repository




Lap time simulation can be an invaluable tool for developing a vehicle. The ability to predict the performance of various vehicle configurations can help guide the engineering design process and ensure that resources are being spent in the areas that will reap the highest reward. On this page, I will discuss the process I used to develop my lap time simulation code, and explain the key decisions I made to achieve my target attributes.

Goals and Objectives
Example output plot of a simulated run on the FSAE Michigan 2019 Endurance Map
The first thing to discuss is what utility you are trying to get out of a lap time simulation, as this drives the major development decisions and what features get included. For my FSAE team, the benefit of a lap sim does not come from being able to perfectly recreate a real world lap time. Rather, the focus is in being able to capture changes in relative performance instead of absolute. As long as the representation of vehicle performance is accurate enough to capture the effect of changes such as reducing weight or improving aerodynamic efficiency, then a lap sim can be used to compare concepts and identify areas of development where we can get the most bang for our buck.
With that in mind, these are the primary objectives identified at the beginning of the project:

Vehicle Path Generation
The first step is to be able to chart a feasible and realistic vehicle trajectory for the lap sim to evaluate. My goal was to re-create the 2019 FSAE Michigan Endurance and Autocross courses. These would be the closest representations of potential future courses that our FSAE cars would run, making them the ideal starting point for performance evaluation. As an added bonus, predicting lap time and comparing to the 2019 score sheets enables us to create points scoring predictions as a means of comparing different concepts.
This is an example of a track map provided by FSAE. There are some cones represented by black dots and a scaling legend, but it is a far cry away from a well defined vehicle path. First, I imported images like these into Solidworks and created a sketch over the image, placing dots over each defined gate cone. I also added more gates to more sharply define the intended course trajectory. I was then able to import the coordinates into an Excel spreadsheet, and properly scale them to match the distance units of interest.

Source: “Endurance 2019.” Fsaeonline.com, Society of Automotive Engineers, Apr. 2019, www.fsaeonline.com/cdsweb/gen/DownloadDocument.aspx?DocumentID=73d7e97f-b223-4a8e-af7d-b7143b5afec2.

Once the points were in excel, I brought them into MATLAB to replicate the track map. At this point, there were enough gates to create a vehicle trajectory. This was defined by a vector the same length as the number of gates, with values between zero and one. Zero meant that the vehicle crossed a given gate right at the very edge of the inside cone, and one meant the vehicle crossed at the absolute outside, and any value in between was an interpolation between the two. These points could be connected to create a fast and distinct definition of vehicle path. On top of that, upper and lower bounds can be automatically updated with vehicle size, allowing a difference in dimensions to affect the final trajectory and helping meet one of the core objectives.
Endurance track represented by gates in MATLAB

This brought a new challenge of finding the best way to connect those dots. MATLAB has a variety of different spline fitting algorithms available, which can create completely different curves from the same sample of points.
Example comparison of available MATLAB Spline fit functions
Source: MathWorks Help Center, MathWorks, 2006, www.mathworks.com/help/matlab/ref/spline.html.

Source: “Smoothing Splines with Different Values for p.” MathWorks Help Center, MathWorks, 2006, www.mathworks.com/help/curvefit/csaps.html.
On top of that, there are a variety of fit parameters, such as the smoothing parameter, that could be adjusted to fine tune the fit. Ultimately finding the best combination was an iterative guess-and-check approach until I found the combination that yielded the most organic and realistic vehicle trajectories. I did this with the help and input of the team drivers, who had much more insight on what the racing line should look like.

Sample of a vehicle autocross trajectory generated using Pchip
The final configuration selected uses the "Pchip" spline fit. Other spline curves had smoother overall curvatures, but were very sensitive to inconsistency in tight areas on the track. Makima, on the other hand, was able to create consistent and repeatable trajectories across many track configurations. The biggest trade-off is the occasional sharp break in curvature. It is important to remember here that no trajectory is going to be perfect, but after review with the drivers it was decided that this method was representational enough to move forward.
The next question is, how do you find the optimal line? It is well accepted that often times, the shortest path through the track is not necessarily the fastest path. However, it makes a good starting spot. To begin with, MATLAB's fmincon function was used to optimize the trajectory to minimize distance traveled, with the constraint that the instantaneous curvature should not exceed the minimum FSAE turn radius at any point along the track. Once the lap sim was operational, it was used as an initial point to optimize the racing line and minimize time elapsed instead of distance traveled.

Example of optimized endurance racing line

Close up between randomly generated (red) trajectory vs optimized (blue) trajectory
Vehicle Performance Modelling
Selecting a vehicle performance modelling method is a critical design decision. Painting in broad brush strokes, it comes down to striking a balance between accuracy of the lap and the computational cost of achieving that accuracy. It is important that lap simulation results reflect realistic vehicle behavior, but it is equally important that a single run doesn't take 48 hours, which would limit opportunities for design space exploration and optimization.
I decided to evaluate vehicle performance in a quasi-steady state approximation. This assumes that the vehicle is simply moving between states of equilibrium at a rate that is slow enough to ignore transient effects. In reality, this is not true. A vehicle is almost always in a transient state, with key parameters such as damping and rotational inertia affecting time domain response. However, transient simulations are often so complex that analytical solutions are impossible, and numerical solutions can be prohibitively expensive in computation time. Using the right size time step, quasi-steady state simulations can maintain a relatively high degree of accuracy for a small fraction of the time cost.

Example of a generated GGV diagram
Quasi-steady state simulations require knowing the steady state capabilities of the vehicle in any given operating condition. This was achieved using a GGV diagram. This is essentially a G-G friction ellipse expanded into 3-D with velocity as the third axis. Each point along the diagram represents a steady state performance condition, and the model discreetly moves from point to point across the diagram.
The implementation of the GGV diagram is the most significant feature of this lap simulation, because it achieves the goals of fast evaluation and modular construction. The lap simulation blindly takes a GGV model input, blind to how that model was generated. This means that different models of varying complexity and scope are interchangeable in the program, so long as the model creates a GGV diagram. This also helps the simulation solve significantly faster, as it eliminates the need to evaluate the performance capabilities of the vehicle in real time as it moves across the track.

Visualization of the forward/reverse method
Source: Criens, C. H. A., Dam, ten, T., Luijten, H. J. C., & Rutjes, T. (2006). Building a MATLAB based Formula Student simulator. (DCT rapporten; Vol. 2006.069). Eindhoven: Technische Universiteit Eindhoven.
The final vehicle states across the track, and subsequent performance, were evaluated using the forward/reverse method, which is visualized on the left. In essence, the vehicle moves forward across the track, and accelerates whenever possible. If it reaches a point of curvature that it is travelling too fast to navigate, the speed immediately drops to the maximum possible. Then, the same process is repeated in reverse, and the final vehicle performance at any point in the track is the minimum of the two. This is significantly more efficient than incorporating complex logic protocols to anticipate corners and braking points.

When all is said and done, this is what the end result looks like!
The most important question is, how well does it work?? Does it accurately represent on-track vehicle performance? Some insight can be gained from the comparison between simulation and logged data below for the 2019 FSAE Michigan Endurance track. The simulation is a representation of Tiger20, the car with which we competed that year, and the logged data comes from our fastest recorded endurance lap.
* Disclaimer: When the final simulation was evaluated, the vehicle distance traveled was about 2-3% off of the published track distance, so the x axis was re-scaled to make the distances match.
Results and Correlation


Note the area to the far left, where the points fall outside of what is otherwise a neat construction of the GGV diagram from actual lap simulation outputs.
What is first apparent is that the correlation is nowhere near perfect. There are a few key differences. For example, the lap simulation drops to much more dramatic minimum velocities. This is attributable to the Makima trajectory that was generated, which featured unrealistic sharp changes in curvature that created local minima in the instantaneous turn radius. This correlates to the point cloud on the right, where the outlier lateral acceleration points correspond to the points when the vehicle entered these outlier points at a proportionally high speed. In addition, the lap sim features much more jagged velocity traces than the logged data. This is due to the nature of the quasi-steady state evaluation, representing an idealized optimal performance where the vehicle can extract the maximum acceleration and braking for a tight sequence of corners where a human driver would instead maintain a more consistent speed. All of this being said, the general trends in both graphs, as well as macro performance statistics, match quite well.
The table below is a testament to the possibilities from using a GGV diagram. The statistics represent the same vehicle configuration navigating the same course, with varying levels of detail and complexity. The orange model is an elementary two-track model, while the blue and green incorporate pitch, roll, and different level of suspension kinematics. As the models increase in detail, the computation time increases. But the similarity in results speaks to the feasibility of using a GGV diagram as a consistent tool for evaluating vehicle performance. This demonstrates the true power of this lap sim as a flexible design tool, which is the ability to pick and choose exactly how much detail you want to include and how much computational efficiency you are willing to give up, without making any changes to the lap simulation code itself.
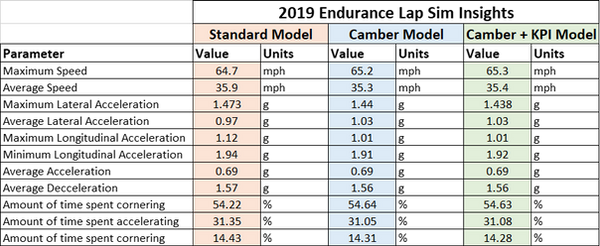
Comparison of lap sim results from different vehicle models with varying levels of complexity
The logged data comparison demonstrates clearly how a quasi-steady state lap simulation with the simplifying assumptions discussed in this page will not capture the true behavior of the vehicle on track. However, comparing the general trends of vehicle performance, the case is also presented that this model is accurate enough to act as a comparison tool to evaluate the performance deltas across various vehicle configurations. Included below are the results from some sensitivity studies used to "gut-check" the efficacy of the program of capturing these performance interactions. To create these results, each 2019 Michigan dynamic event track was captured and evaluated, in order to predict the total dynamic event points scored as an ultimate comparison.




Some event-specific results displaying the sensitivity of vehicle performance to different aerodynamic lift and drag configurations
Conclusion and Future Development
The general accuracy of the endurance lap when compared to logged data, as well as the reasonable results from the sensitivity analyses, demonstrate the usefulness of this lap simulation as a tool to evaluate and compare various design configurations. However, further validation can be carried out, including different track configurations and vehicle characteristics. For example, lap times could be taken with increasing amounts of ballast in the cockpit to evaluate whether the lap sim is properly predicting the proportional performance loss or not.
In addition, I would like to explore future opportunities to re-introduce transient effects into this simulation. Another simulation currently in the team's repertoire is a 7 DoF ride model, though it is still in need of some fine tuning. The velocity and acceleration outputs from the lap sim could be combined with a road surface profile as an input to this model, generating a time history of the normal loads on each tire throughout the course. This can be used to generate scaling factors for the GGV diagram as a function of position along the track. This updated GGV diagram can be used to re-evaluate the lap sim, with the results in turn being fed back into the ride model. This process can be repeated until the lap simulation results converge with the updated GGV predictions. This would be a "quasi-transient" method of sorts, and would ignore factors such as driver control models, but it can easily be incorporated into the existing simulation architecture and would provide a valuable approximation that can help evaluate the effects of dampers, center of pressure migration, and many more variables!
One of my friends was kind enough to take my files and documentation and create a GitHub repository! If you are interested in exploring the lap sim in greater detail, be sure to check that out!


